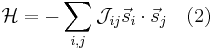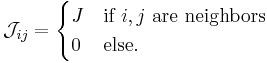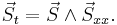Classical Heisenberg model

The Classical Heisenberg model is the 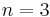$n = 3$ case of the n-vector model, one of the models used in statistical physics to model ferromagnetism, and other phenomena.

1 Definition
2 Properties
3 See also
4 References
5 External links

Definition

It can be formulated as follows: take a d-dimensional lattice, and a set of spins of the unit length

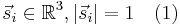$\vec{s}_i \in \mathbb{R}^3, |\vec{s}_i|=1\quad (1)$ ,

each one placed on a lattice node.

The model is defined through the following Hamiltonian:

$\mathcal{H} = -\sum_{i,j} \mathcal{J}_{ij} \vec{s}_i \cdot \vec{s}_j\quad (2)$

with

$\mathcal{J}_{ij} = \begin{cases} J & \mbox{if }i, j\mbox{ are neighbors} \\ 0 & \mbox{else.}\end{cases}$

a coupling between spins.

Properties

Polyakov has conjectured that, in dimension 2, as opposed to the classical XY model, there is no dipole phase for any 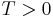$T>0$ ; i.e. at non-zero temperature the correlations cluster exponentially fast.^[1]

The general mathematical formalism used to describe and solve the Heisenberg model and certain generalizations is developed in the article on the Potts model.

In the continuum limit the Heisenberg model (2) gives the following equation of motion

$\vec{S}_{t}=\vec{S}\wedge \vec{S}_{xx}.$

This equation is called the continuous classical Heisenberg ferromagnet equation or shortly Heisenberg model and is integrable in the soliton sense. It admits several integrable and nonintegrable generalizations like Landau-Lifshitz equation, Ishimori equation and so on.

References

^ Polyakov, A.M. (1975). Phys.Letts. B 59. Bibcode 1975PhLB...59...79P. doi:10.1016/0370-2693(75)90161-6. http://www.sciencedirect.com/science/article/pii/0370269375901616.

Classical Heisenberg model

Contents

Definition

Properties

See also

References

External links